LÝ THUYẾT VÀ CÁC DẠNG BÀI TẬP ĐIỆN TRƯỜNG
A. TÓM TẮT LÝ THUYẾT
1. Khái niệm điện trường: Là môi trường tồn tại xung quanh điện tích và tác dụng lực lên điện tích khác đặt trong nó.
2. Cường độ điện trường: Là đại lượng đặc trưng cho điện trường về khả năng tác dụng lực.

Đơn vị: E (V/m)
q > 0 : 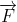 cùng phương, cùng chiều với
cùng phương, cùng chiều với 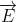 .
.
q < 0 : 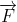 cùng phương, ngược chiều với
cùng phương, ngược chiều với 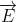 .
.
3. Véctơ cường độ điện trường do 1 điện tích điểm Q gây ra tại một điểm M cách Q một đoạn r có:
- Điểm đặt: Tại M.
- Phương: đường nối M và Q
- Chiều: Hướng ra xa Q nếu Q > 0
Hướng vào Q nếu Q <0
- Độ lớn:  với k = 9.109
với k = 9.109
- Biểu diễn:
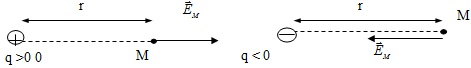
5. Nguyên lý chồng chất điện trường: Giả sử có các điện tích q1, q2,…..,qn gây ra tại M các vector cường độ điện trường  thì vector cường độ điện trường tổng hợp do các điện tích trên gây ra tuân theo nguyên lý chồng chất điện trường
thì vector cường độ điện trường tổng hợp do các điện tích trên gây ra tuân theo nguyên lý chồng chất điện trường  .
.
B. CÁC DẠNG BÀI TẬP
Dạng 1: Xác định cường độ điện trường do điện tích gây ra tại một điểm
Phương pháp:
Cường độ điện trường do điện tích điểm Q gây ra có:
+ Điểm đặt: Tại điểm đang xét;
+ Phương: Trùng với đường thẳng nối điện tích Q và điểm đang xét;
+ Chiều: Hướng ra xa Q nếu Q > 0 và hướng về Q nếu Q < 0;
+ Độ lớn: E = k , trong đó k = 9.109Nm2C-2.
, trong đó k = 9.109Nm2C-2.
Dạng 2: Xác định lực điện trường tác dụng lên một điện tích trong điện trường
Phương pháp:
Lực tĩnh điện tác dụng lên điện tích q đặt trong điện trường: 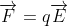
có: + Điểm đặt: tại điểm đặt điện tích q;
+ Phương: trùng phương với vector cường độ điện trường ;
+Chiều: Cùng chiều với nếu q > 0 và ngược chiều với nếu q < 0;
+ Độ lớn: F = 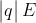
Dạng 3: Xác định cường độ điện trường tổng hợp do nhiều điện tích gây ra tại một điểm.
Phương pháp: sử dụng nguyên lý chồng chất điện trường.
- Áp dụng nguyên lí chồng chất điện trường:  .
.
- Biểu diễn  bằng các vecto.
bằng các vecto.
- Vẽ vecto hợp lực bằng theo quy tắc hình bình hành.
- Tính độ lớn hợp lực dựa vào phương pháp hình học hoặc định lí hàm số cosin.
* Các trường hợp đặ biệt:
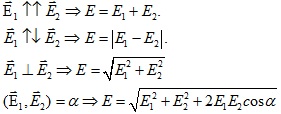
C. BÀI TẬP VẬN DỤNG
Bài 1: Một điện tích Q = 10-6C đặt trong không khí:
a. Xác định cường độ điện trường tại điểm cách điện tích 30cm.
b. Đặt điện tích trong chất lỏng có hằng số điện môi  = 16. Điểm có cường độ điện trường như câu a cách điện tích bao nhiêu?.
= 16. Điểm có cường độ điện trường như câu a cách điện tích bao nhiêu?.
Bài 2: Hai điện tích điểm q1 = 4.10-8C và q2 = - 4.10-8C nằm cố định tại hai điểm AB cách nhau 20 cm trong chân không.
1. Tính lực tương tác giữa 2 điện tích.
2. Tính cường độ điện trường tại:
a. điểm M là trung điểm của AB.
b. điểm N cách A 10cm, cách B 30 cm.
c. điểm I cách A 16cm, cách B 12 cm.
d. điểm J nằm trên đường trung trực của AB cách AB một đoạn 10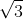 cm
cm
Hướng dẫn:
1. Lực tương tác giữa 2 điện tích:
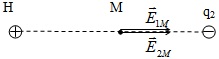
2. Cường độ điện trường tại M:
a. Vectơ cường độ điện trường  do điện tích q; q2 gây ra tại M có:
do điện tích q; q2 gây ra tại M có:
- Điểm đặt: Tại M.
- Phương, chiều: như hình vẽ
- Độ lớn : 
Vectơ cường độ điện trường tổng hợp: 
Vì  cùng phương, cùng chiều với
cùng phương, cùng chiều với  nên ta có E = E1M + E2M =
nên ta có E = E1M + E2M = 
Vectơ cường độ điện trường tổng hợp: 
Vì  cùng phương, ngược chiều với
cùng phương, ngược chiều với  nên ta có
nên ta có 
Bài 3 : Tại hai điểm A và B đặt hai điện tích điểm q1 = 20 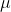 Cvà q2 = -10
Cvà q2 = -10 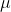 C cách nhau 40 cm trong chân không.
C cách nhau 40 cm trong chân không.
a) Tính cường độ điện trường tổng hợp tại trung điểm AB.
b) Tìm vị trí cường độ điện trường gây bởi hai điện tích bằng 0 ?
Hướng dẫn :
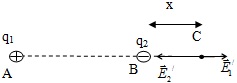
b) Gọi C là điểm có cường độ điện trường tổng hợp 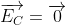
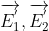 là vecto cường độ điện trường do q1 và q2 gây ra tại C.
là vecto cường độ điện trường do q1 và q2 gây ra tại C.
Có : 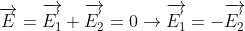
Do |q1| > |q2| nên C nằm gần q2
Đặt CB = x  AC = 40 + x, có :
AC = 40 + x, có : 
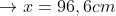
Bài 4 : Hai điện tích điểm q1 = 1.10-8 C và q2 = -1.10-8 C đặt tại hai điểm A và B cách nhau một khoảng 2d = 6cm. Điểm M nằm trên đường trung trực AB, cách AB một khoảng 3 cm.
a) Tính cường độ điện trường tổng hợp tại M.
b) Tính lực điện trường tác dụng lên điện tích q = 2.10-9 C đặt tại M.
Bài 5 : Tại 3 đỉnh hình vuông cạnh a = 20 cm, ta đặt 3 điện tích cùng độ lớn q1 = q2 = q3 = 3.10 -6 C.
a. Tính cường độ điện trường tổng hợp tại tâm hình vuông ?
b. Tại đỉnh thứ 4 hình vuông
c. Tính lực điện tác dụng lên điện tích q4 = 8.10-8C đặt tại đỉnh thứ 4 này.
Bài 6 : Một quả cầu nhỏ khối lượng m = 1g, mang điện tích q = 10-5 C, treo bằng sợi dây mảnh và đặt trong điện trường đều E. Khi quả cầu nằm cân bằng thì dây treo hợp với phương thẳng đứng một góc . Xác định cường độ điện trường E, biết g = 10m/s2.
ĐS : E = 1730 V/m.
Bài 7 : Một điện tích điểm q = 2.10-6C đặt cố định trong chân không.
a) Xác định cường độ điện trường tại điểm cách nó 30 cm ?
b) Tính độ lớn lực điện tác dụng lên điện tích 1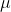 C đặt tại điểm đó ?
C đặt tại điểm đó ?
c) Trong điện trường gây bởi q, tại một điểm nếu đặt điện tích q1 = 10-4 C thì chịu tác dụng lực là 0,1 N. Hỏi nếu đặt điện tích q2 = 4.10-5 C thì lực điện tác dụng là bao nhiêu ?
ĐS : a) 2.105 V/m, b) 0,2 N, c) 0,04 N
Bài 8: Một điện tích q = -10-7C đặt tại điểm N trong điện trường của một điện tích Q thì chịu tác dụng của lực điện F = 3.10-3N.
a) Tìm cường độ điện trường E tại điểm N.
b) Xác định điện tích Q? Biết rằng vectơ cường độ điện trường tại điểm N có chiều hướng vào điện tích Q và NQ = 3cm.
ĐIỆN TRƯỜNG DO MỘT ĐIỆN TÍCH ĐIỂM GÂY RA
A.LÍ THUYẾT
* Phương pháp:
-Nắm rõ các yếu tố của Véctơ cường độ điện trường do một điện tích điểm q gây ra tại một điểm cách điện tích khoảng r:
+ điểm đặt: tại điểm ta xét
+ phương: là đường thẳng nối điểm ta xét với điện tích
+ Chiều: ra xa điện tích nếu q > 0, hướng vào nếu q < 0
+ Độ lớn: 
- Lực điện trường: 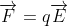 , độ lớn
, độ lớn 
Nếu q > 0 thì 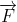 cùng hướng với
cùng hướng với 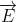 ; Nếu q < 0 thì
; Nếu q < 0 thì 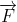 ngược hướng với
ngược hướng với 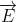
Chú ý: Kết quả trên vẫn đúng với điện trường ở một điểm bên ngoài hình cầu tích điện q, khi đó ta coi q là một điện tích điểm đặt tại tâm cầu.
Bài 1. Một điện tích điểm q = 10-6C đặt trong không khí
a. Xác định cường độ điện trường tại điểm cách điện tích 30cm, vẽ vectơ cường độ điện trường tại điểm này
b. Đặt điện tích trong chất lỏng có hằng số điện môi ε = 16. Điểm có cường độ điện trường như câu a cách điện tích bao nhiêu.
Bài 2: Cho hai điểm A và B cùng nằm trên một đường sức của điện trường do một điện tích điểm q > 0 gây ra. Biết độ lớn của cường độ điện trường tại A là 36V/m, tại B là 9V/m.
a. Xác định cường độ điện trường tại trung điểm M của AB.
b. Nếu đặt tại M một điện tích điểm q0 = -10-2C thì độ lớnn lực điện tác dụng lên q0 là bao nhiêu? Xác định phương chiều của lực.

Hướng dẫn giải:
Ta có:
 (1)
(1)
 (2)
(2)
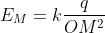 (3)
(3)
Lấy (1) chia (2) 
Lấy (3) chia (1) 
Với: 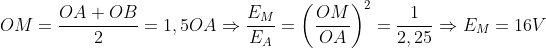
b. Lực từ tác dụng lên qo: 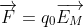
vì q0 < 0 nên 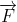 ngược hướng với
ngược hướng với  và có độ lớn:
và có độ lớn: 
Bài 3:Quả cầu kim loại bán kính R = 5cm được tích điện q,phân bố đều.Đặt σ = q/S là mật độ điện mặt, S là diện tích hình cầu. Cho σ = 8,84. 10-5C/m2. Tính độ lớn cường độ điện trường tại điểm cách mặt cầu 5cm?
ĐS: E=2,5.106 (V/m)
(Chú ý công thức tính diện tích xung quanh của hình cầu:S=4πR2)
CƯỜNG ĐỘ ĐIỆN TRƯỜNG DO NHIỀU ĐIỆN TÍCH ĐIỂM GÂY RA
Bài 1: Cho hai điện tích q1 = 4.10-10C, q2 = -4.10-10C đặt ở A,B trong không khí, AB = a = 2cm. Xác định véc tơ cường độ điện trường tại:
a) H là trungđiểm của AB.
b) M cách A 1cm, cách B 3cm.
c) N hợp với A,B thành tam giác đều.
ĐS: a.72.103(V/m); b.32. 103(V/m); c.9000(V/m)
Bài 2: Hai điện tích q1 = 8.10-8C, q2 = -8.10-8C đặt tại A, B trong không khí, AB=4cm. Tìm véctơ cường độ điện trường tại C với:
a) CA = CB = 2cm.
b) CA = 8cm; CB = 4cm.
c) C trên trung trực AB, cách AB 2cm, suy ra lực tác dụng lên q = 2.10-9C đặt tại C.
ĐS: E song song với AB, hướng từ A tới B có độ lớn E = 12,7.105V/m; F = 25,4.10-4N)
Bài 3: Hai điện tích +q và – q (q >0) đặt tại hai điểm A và B với AB = 2a. M là một điểm nằm trên đường trung trực của AB cách AB một đoạn x.
a. Xác định vectơ cường độ điện trường tại M
b. Xác định x để cường độ điện trường tại M cực đại, tính giá trị đó
Hướng dẫn giải:
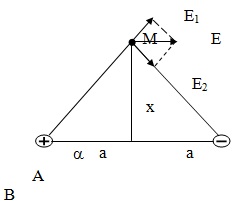
a. Cường độ điện trường tại M: 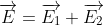
ta có: 
Hình bình hành xác định là hình thoi: 
b. Từ (1) Thấy để Emax thì x = 0: Emax = 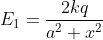
c) Lực căng dây: 
Bài 4 Hai điện tích q1 = q2 = q > 0 đặt tại A và B trong không khí. cho biết AB = 2a
a) Xác định cường độ điện trường tại điểm M trên đường trung trực của AB cách Ab một đoạn h.
b) Định h để EM cực đại. Tính giá trị cực đại này.
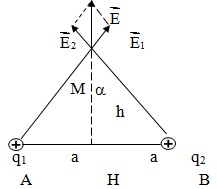
Hướng dẫn giải:
a) Cường độ điện trường tại M: 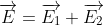
Ta có: 
Hình bình hành xác định là hình thoi: 
b) Định h để EM đạt cực đại: ![a^{2}+h^{2}=\frac{a^{2}}{2}+\frac{a^{2}}{2}+h^{2}\geq 3.\sqrt[3]{\frac{a^{4}h^{2}}{4}}](http://latex.codecogs.com/gif.latex?a%5E%7B2%7D+h%5E%7B2%7D=%5Cfrac%7Ba%5E%7B2%7D%7D%7B2%7D+%5Cfrac%7Ba%5E%7B2%7D%7D%7B2%7D+h%5E%7B2%7D%5Cgeq&space;3.%5Csqrt%5B3%5D%7B%5Cfrac%7Ba%5E%7B4%7Dh%5E%7B2%7D%7D%7B4%7D%7D)

Do đó: 
EM đạt cực đại khi: 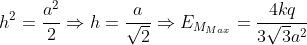
Bài 5 Tại 3 đỉnh ABC của tứ diện đều SABC cạnh a trong chân không có ba điện ích điểm q giống nhau (q<0). Xác định điện trường tại đỉnh S của tứ diện. (ĐS:  )
)
Bài 6 Hình lập phương ABCDA’B’C’D’ cạnh a trong chân không. Hai điện tích  đặt ở A, C, hai điện tích
đặt ở A, C, hai điện tích  đặt ở B’ và D’. Tính độ lớn cường độ điện trường tại tâm O của hình lập phương. (ĐS:
đặt ở B’ và D’. Tính độ lớn cường độ điện trường tại tâm O của hình lập phương. (ĐS:  )
)
CHUYỂN ĐỘNG CỦA ĐIỆN TÍCH ĐIỂM TRONG ĐIỆN TRƯỜNG ĐỀU
A.LÍ THUYẾT
Một điện tích điểm q dương, khối lượng m bay vào điện trường đều tại điểm M (Điện trường đều được tạo bởi hai bản kim loại phẳng rộng đặt song song, đối diện nhau, hai bản được tích điện trái dấu và bằng nhau về độ lớn) với vận tốc ban đầu 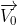 tạo với phương của đường sức điện một góc
tạo với phương của đường sức điện một góc  . Lập phương trình chuyển động của điện tích q, Viết phương trình quĩ đạo của điện tích q rồi xét các trường hợp của góc
. Lập phương trình chuyển động của điện tích q, Viết phương trình quĩ đạo của điện tích q rồi xét các trường hợp của góc  .
.
Cho biết: Điện trường đều có véctơ cường độ điện trường là 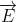 , M cách bản âm một khoảng b(m), bản kim loại dài l(m), Hai bản cách nhau d(m), gia tốc trọng trường là g.
, M cách bản âm một khoảng b(m), bản kim loại dài l(m), Hai bản cách nhau d(m), gia tốc trọng trường là g.
Lời giải:

**Chọn hệ trục tọa độ 0xy:
Gốc 0 trùng với M.
0x: theo phương ngang(Vuông góc với các đường sức)
0y: theo phương thẳng đứng từ trên xuống dưới (Cùng phương, chiều với đường sức)
Gọi α là góc mà vectơ vận tốc ban đầu của điện
Tích hợp với phương thẳng đứng.
* Lực tác dụng: Trọng lực 
Lực điện: 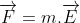
Hai lực này có phương, chiều cùng phương chiều với.Đường sức điện (Cùng phương chiều với trục 0y). Phân tích chuyển động của q thành hai chuyển động thành phần theo hai trục 0x và 0y.
1. Xét chuyển động của q trên phương 0x.
Trên phương này q không chịu bất kì một lực nào nên q
Sẽ chuyển động thẳng đều trên trục 0x với vận tốc không
đổi: gia tốc ax=0, Vx= V0x =V0.sinα (1)
=>Phương trình chuyển động của q trên trục 0x: x= Vx.t= V0.sinα.t (2)
2. Xét chuyển động của q theo phương 0y:
- Theo phương 0y: q chịu tác dụng của các lực không đổi(Hợp lực cũng không đổi) q thu được gia tốc
 (3)
(3)
- Vận tốc ban đầu theo phương 0y:V0y= V0.cosα (4)
*Vận tốc của q trên trục 0y ở thời điểm t là: Vy= V0y+ a.t = V0.cosα+  .t (5)
.t (5)
=> Phương trình chuyển động của q trên trục 0y: y = V0.cosα.t +  .t2 (6)
.t2 (6)
TÓM LẠI: Đặc điểm chuyển động của q trên các trục là:

** Phương trình quĩ đạo chuyển động của điện tích q là khử t ở phương trình tọa độ theo trục 0y bằng cách rút
t = 
y = V0.cosα.  (7)
(7)
y = cotgα.x +  (8)
(8)
Vậy quĩ đạo của q có dạng là một Parabol (Trừ nhận giá trị góc 00, 1800 sẽ nêu ở dưới)
Chú ý:Bài toán chuyển động của e thường bỏ qua trọng lực.
B.CÁC DẠNG BÀI TẬP(XÉT CHO Q>0)
DẠNG 1: VECTƠ VẬN TỐC CỦA ĐIỆN TÍCH CÙNG HƯỚNG ĐƯỜNG SỨC
a. Góc =0 (Ban đầu q chuyển động vào điện trường theo hướng của đường sức)
Trường hợp này 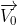 cùng hướng với
cùng hướng với 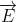 .
.
Dựa vào (I), (II). Ta có:



v0 hướng cùng chiều dương, xét tổng hợp lực theo 0y, nếu nó hướng cùng chiều dương thì vật chuyển động nhanh dần đều.
1. Thời gian mà q đến bản âm: khi đó y= b => b=  (9)
(9)
2. Vận tốc khi q đập vào bản âm là V xác định theo 2 cách:
C1: Thay t ở (9) vào vào công thức vận tốc của IV=> V
C2: Áp dụng công thức liên hệ giữa vận tốc, gia tốc và đường đi trong chuyển động thẳng nhanh dần đều:
2.a.S = V2 - V02 tức là 2.a.b = V2 - V02 (10)
v0 hướng cùng chiều dương, xét tổng hợp lực theo 0y, nếu nó hướng ngược chiều dương thì vật chuyển động chậm dần đều đến khi v=0 thì chuyển động nhanh dần đều theo hướng nguợc lại.
II.BÀI TẬP VẬN DỤNG
Bài 1: Giữa 2 bản của tụ điện đặt nằm ngang cách nhau d = 40 cm có một điện trường đều E = 60V/m. Một hạt bụi có khối lượng m = 3g và điện tích q = 8.10-5C bắt đầu chuyển động từ trạng thái nghỉ từ bản tích điện dương về phía tấm tích điện âm. Bỏ qua ảnh hưởng của trọng trường. Xác định vận tốc của hạt tại điểm chính giữa của tụ điện
ĐS:v=0,8m/s
Bài 2: Một electron bay vào trong một điện trường theo hướng ngược với hướng đường sức với vận tốc 2000km/s. Vận tốc của electron ở cuối đoạn đường sẽ là bao nhiêu nếu hiệu điện thế ở cuối đoạn đường đó là 15V.
ĐS:v=3,04.10 6 m/s
Bài 3: Một electron bắt đầu chuyển động dọc theo chiều đường sức điện trường của một tụ điện phẳng, hai bản cách nhau một khoảng d = 2cm và giữa chúng có một hiệu điện thế U = 120V. Electron sẽ có vận tốc là bai nhiêu sau khi dịch chuyển được một quãng đường 1cm.
Bài 4: Một electron bay vào điện trường của một tụ điện phẳng theo phương song song cùng hướng với các đường sức điện trường với vận tốc ban đầu là 8.106m/s. Hiệu điện thế tụ phải có giá trị nhỏ nhất là bao nhiêu để electron không tới được bản đối diện
ĐS:U 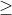 182V
182V
Bài 5: Hại bụi có m=10-12 g nằm cân bằng giữa điện trường đều giữa hai bản tụ.Biết U=125V và d=5cm.
a.Tính điện tích hạt bụi?
b.Nếu hạt bụi mất đi 5e thì muốn hạt bụi cân bằng , U=?
DẠNG 2: VECTƠ VẬN TỐC CỦA ĐIỆN TÍCH NGƯỢC HƯỚNG ĐƯỜNG SỨC
I.LÍ THUYẾT
b. Góc =1800 (Ban đầu q vào điện trường ngược hướng đường sức). Trường hợp này 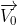 ngược hướng với véc tơ cường độ điện trường
ngược hướng với véc tơ cường độ điện trường 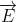 .
.
Dựa vào I, II ta có:



Nếu tổng hợp lực điện và trọng lực trên phương Oy mà hướng cùng Oy thì vật chuyển động theo hai quá trình.
+ Quá trình 1: q chuyển động thẳng chậm dần đều ngược chiều dương trục oy:
Giả sử: Khi đến N thì q dừng lại, quá trình này diễn ra trong thời gian t1 thỏa mãn:
 (11)
(11)
Quãng đường MN=S được xác định: 2.a.S = V2- V02 = - V02 (12)
(V0 trong trường hợp này lấy giá trị âm vìngược hướng 0y).
* Nếu S > d - b thì q chuyển động thẳng chậm dần đều ngược chiều dương trục 0y và đập vào bản dương gây ra va chạm.
Ở đây a chỉ xét S < d- b (Điểm N vẫn nằm trong khoảng không gian giữa hai bản)
+ Quá trình 2: Tại N điện tích q bắt đầu lại chuyển động thẳng nhanh dần đều theo trục 0y. Với vận tốc tại N bằng không, gia tốc  và bài toán như trường hợp
và bài toán như trường hợp  = 0.
= 0.
Nếu tổng hợp lực điện và trọng lực trên phương Oy mà ngược hướng cùng Oy thì vật chuyển động nhanh dần đều theo hướng ngược Oy.
II.BÀI TẬP VẬN DỤNG
1. Một e có vận tốc ban đầu vo = 3. 106 m/s chuyển động dọc theo chiều đường sức của một điện trường có cường độ điện trường E = 1250 V/m. Bỏ qua tác dụng của trọng trường, e chuyển động như thế nào?
Đ s: a = -2,2. 1014 m/s2, s= 2 cm.
2. Một e chuyển động với vận tốc ban đầu 104 m/s dọc theo đường sức của một điện trường đều được một quảng đường 10 cm thì dừng lại.
a. Xác định cường độ điện trường.
b. Tính gia tốc của e.
Đ s: 284. 10-5 V/m, 5. 107m/s2.
3. Một e chuyển động dọc theo đường sức của một điện trường đều có cường độ 364 V/m. e xuất phát từ điểm M với vận tốc 3,2. 106 m/s. Hỏi:
a. e đi được quảng đường dài bao nhiêu thì vận tốc của nó bằng 0 ?
b. Sau bao lâu kể từ lúc xuất phát e trở về điểm M ?
Đ s: 0,08 m, 0,1 ms
4: Một electron bay từ bản âm sang bản dương của một tụ điện phẳng. Điện trường trong khoảng hai bản tụ có cường độ E=6.104V/m. Khoảng cách giưac hai bản tụ d =5cm.
a. Tính gia tốc của electron. (1,05.1016 m/s2)
b. tính thời gian bay của electron biết vận tốc ban đầu bằng 0. (3ns)
c. Tính vận tốc tức thời của electron khi chạm bản dương. (3,2.107 m/s2)
5: Giữa hai bản kim loại đặt song song nằm ngang tích điện trái dấu có một hiệu điện thế U1=1000V khoảng cách giữa hai bản là d=1cm. Ở đúng giưã hai bản có một giọt thủy ngân nhỏ tích điện dương nằm lơ lửng. Đột nhiên hiệu điện thế giảm xuống chỉ còn U2 = 995V. Hỏi sau bao lâu giọt thủy ngân rơi xuống bản dương?
CƯỜNG ĐỘ ĐIỆN TRƯỜNG TỔNG HỢP TRIỆT TIÊU
BÀI TẬP VẬN DỤNG:
Bài 1: Cho hai điện tích điểm cùng dấu có độ lớn  = 4
= 4 đặt tại a,b cách nhau 12cm. Điểm có vectơ cường độ điện trường do
đặt tại a,b cách nhau 12cm. Điểm có vectơ cường độ điện trường do  và
và  gây ra bằng nhau ở vị trí ( Đs:
gây ra bằng nhau ở vị trí ( Đs: 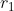 = 24cm,
= 24cm, 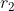 = 12cm)
= 12cm)
Bài 2: Cho hai điện tích trái dấu ,có độ lớn điện tích bằng nhau, đặt tại A,B cách nhau 12cm .Điểm có vectơ cường độ điện trường do  và
và  gây ra bằng nhau ở vị trí ( Đs:
gây ra bằng nhau ở vị trí ( Đs: 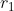 =
= 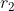 = 6cm)
= 6cm)
Bài 3: Cho hai điện tích  =
=  C,
C, 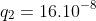 C đặt tại A, B cách nhau 5cm . Điểm có vec tơ cương độ điện trường vuông góc với nhau và E1 = E2 ( Đs:
C đặt tại A, B cách nhau 5cm . Điểm có vec tơ cương độ điện trường vuông góc với nhau và E1 = E2 ( Đs: 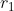 = 3cm,
= 3cm, 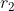 = 4cm)
= 4cm)
Bài 4: Tại ba đỉnh A,B,C của hình vuông ABCD cạnh a = 6cm trong chân không, đặt ba điện tích điểm  =
=  = 2.10-7C và
= 2.10-7C và  = - 4.10-7C. Xác định điện tích q4 đặt tại D để cường độ điện trường tổng hợp gây bởi hệ điện tích tại tâm O của hìnhvuông bằng 0. (
= - 4.10-7C. Xác định điện tích q4 đặt tại D để cường độ điện trường tổng hợp gây bởi hệ điện tích tại tâm O của hìnhvuông bằng 0. (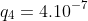 C)
C)
Bài 5: Cho hình vuông ABCD, tại A và C đặt các điện tích  =
=  = q. Hỏi phải đặt ở B điện tích bao nhiêu để cường độ điện trường ở D bằng không. (ĐS:
= q. Hỏi phải đặt ở B điện tích bao nhiêu để cường độ điện trường ở D bằng không. (ĐS:  )
)
Bài 6: Tại hai đỉnh A,B của tam giác đều ABC cạnh a đặt hai điện tích điểm  trong không khí. Hỏi phải đặt điện tích
trong không khí. Hỏi phải đặt điện tích  có giá trị bao nhiêu tại C để cường độ điện trường gây bởi hệ 3 điện tích tại trọng tâm G của tam giác bằng0. (
có giá trị bao nhiêu tại C để cường độ điện trường gây bởi hệ 3 điện tích tại trọng tâm G của tam giác bằng0. ( 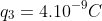 )
)
Bài 7: Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh AD = a = 3cm, AB = b = 4cm. Các điện tích q1, q2, q3 được đặt lần lượt tại A, B, C. Biết q2 = -12,5.10-8C và cường độ điện trường tổng hợp tại D bằng 0. Tính q1, q2.
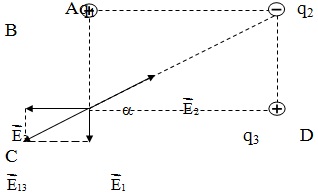
Hướng dẫn giải:
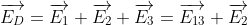
Vì q2 < 0 nên q1, q3 phải là điện tích dương. Ta có:

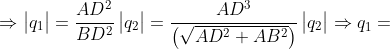

Tương tự: 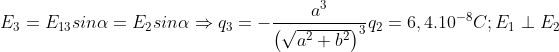
Bài toán tổng quát:
Hai điện tích  ,
,  đặt tại hai điểm A,B trong môi trường đồng chất có hằng số điện môi
đặt tại hai điểm A,B trong môi trường đồng chất có hằng số điện môi  và cách nhau một khoảng AB = r. Hãy tìm điểm mà cường độ điện trường tổng hợp tại đó do
và cách nhau một khoảng AB = r. Hãy tìm điểm mà cường độ điện trường tổng hợp tại đó do  ,
,  gây ra bằng không.
gây ra bằng không.
Chú ý: Đây là bài toán tổng quát, khi giải bài này cần làm tổng quát sau đó đưa ra các bài toán con để áp dụng cụ thể.
Giải:
Các bước giải bài toán :
Gọi điểm cần tìm là C mà tại đó cường độ điện trường tổng hợp do  ,
,  gây ra bằng không.
gây ra bằng không.
Theo đề bài ta có:
 (1)
(1)
( Hai vectơ  là hai vectơ đối ).
là hai vectơ đối ).
Từ (1)  cùng phương
cùng phương  C thuộc đường thẳng AB.
C thuộc đường thẳng AB.
Từ (1) 
Hay  (2)
(2)
(Từ (2)  C sẽ nằm xa điện tích có độ lớn lớn hơn).
C sẽ nằm xa điện tích có độ lớn lớn hơn).
Từ (1)  ngược chiều
ngược chiều 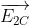
Xét trường hợp 1:  ,
,  cùng dấu (
cùng dấu ( .
. 
 )
)  C nằm trong đoạn thẳng AB
C nằm trong đoạn thẳng AB  AC+CB = AB (a)
AC+CB = AB (a)
Xét trường hợp 2:  ,
,  trái dấu (
trái dấu ( .
. 
 )
)  C nằm ngoài đoạn AB.
C nằm ngoài đoạn AB.
Từ (2) ta có các trường hợp cụ thể sau:
Xét trường hợp 2.1: 
 C nằm lệch về phía trái của đoạn AB
C nằm lệch về phía trái của đoạn AB  CA+AB = CB (b)
CA+AB = CB (b)
Xét trường hợp 2.2: 
 C nằm lệch về phía phải của đoạn AB
C nằm lệch về phía phải của đoạn AB  AB+BC = AC (c)
AB+BC = AC (c)
Kết hợp (2) với (a) hoặc (b) hoặc (c), tùy trường hợp để giải và tìm ra AC, AB và kết luận.
Chú ý: -Vì trong mọi trường hợp đều có  nên khi cho đề giáo viên cần chú ý tỉ số của
nên khi cho đề giáo viên cần chú ý tỉ số của  và
và  sao cho
sao cho  là một số tự nhiên thì bài toán trở nên tròn số và đơn giản.
là một số tự nhiên thì bài toán trở nên tròn số và đơn giản.
- Lúc dạy giáo viên nên đi từ từ các bước kèm theo lí luận bằng hình vẽ sao cho học sinh dễ hiểu nhất. Đây là bài toán thuộc dạng tương đối khó với học sinh vì dài và liên quan đến kiến thức về vectơ.
- Đối với trường hợp  = -
= -  thì sẽ không tìm được vị trí mà tại đó cường độ điện trường tổng hợp do gây ra bằng không.
thì sẽ không tìm được vị trí mà tại đó cường độ điện trường tổng hợp do gây ra bằng không.
CÁC BÀI TOÁN CỤ THỂ
Bài 1: Cho hai điện tích  đặt tại hai điểm A,B trong chân không cách nhau một khoảng AB =30cm.Tìm những điểm mà tại đó cường độ điện trường tổng hợp do
đặt tại hai điểm A,B trong chân không cách nhau một khoảng AB =30cm.Tìm những điểm mà tại đó cường độ điện trường tổng hợp do  ,
,  gây ra bằng không.
gây ra bằng không.
Chú ý: Đây là bài toán cụ thể trong trường hợp 1 của bài toán trên.
Giải:

Gọi điểm cần tìm là C mà tại đó cường độ điện trường tổng hợp do  ,
,  gây ra bằng không. Theo đề bài ta có:
gây ra bằng không. Theo đề bài ta có:
 (1)
(1)
( Hai vectơ  là hai vectơ đối ).
là hai vectơ đối ).
Từ (1)  cùng phương
cùng phương  C thuộc đường thẳng AB.
C thuộc đường thẳng AB.
Từ (1)  ngược chiều
ngược chiều 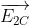 và
và  ,
,  cùng dấu (
cùng dấu ( .
. 
 )
)
 C nằm trong đoạn thẳng AB
C nằm trong đoạn thẳng AB  AC + CB = AB (2)
AC + CB = AB (2)
Từ (1) 
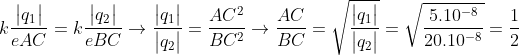
Hay BC = 2AC (3).
Từ (2) và (3) giải ra ta có kết quả: AC = 10cm, BC = 20cm.
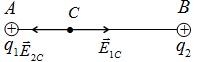
Kết luận: Vậy điểm C cần tìm cách nằm trong đoạn thẳng AB và cách A 10cm, cách B 20cm như hình vẽ.
Bài 2: Hai điện tích  đặt tại hai điểm A,B trong chân không cách nhau một khoảng AB =20cm.Tìm những điểm mà tại đó cường độ điện trường tổng hợp tại đó do
đặt tại hai điểm A,B trong chân không cách nhau một khoảng AB =20cm.Tìm những điểm mà tại đó cường độ điện trường tổng hợp tại đó do  ,
,  gây ra bằng không.
gây ra bằng không.
Chú ý: Đây là bài toán cụ thể trong trường hợp 21 của bài toán tổng quát trên.
Giải:
Gọi điểm cần tìm là C mà tại đó cường độ điện trường tổng hợp do  ,
,  gây ra bằng không. Theo đề bài ta có:
gây ra bằng không. Theo đề bài ta có:
 (1)
(1)
( Hai vectơ  là hai vectơ đối ).
là hai vectơ đối ).
Từ (1)  cùng phương
cùng phương  C thuộc đường thẳng AB.
C thuộc đường thẳng AB.
Từ (1)  ngược chiều
ngược chiều 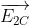 và
và  ,
,  trái dấu (
trái dấu ( .
. 
 ) và
) và 
 C nằm lệch về phía trái của
C nằm lệch về phía trái của
đoạn AB  CA + AB = CB (2)
CA + AB = CB (2)
Từ (1) 
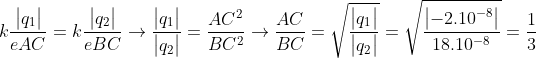
Hay BC = 3AC (3).
Từ (2) và (3) giải ra ta có kết quả: AC = 10cm, BC = 30cm.

Kết luận: Vậy điểm C cần tìm cách nằm trên đường thẳng AB và nằm lệch về phía trái của (AB) và cách A 10cm, cách B 30cm như hình vẽ.
Điểm có cường độ điện trường tổng hợp tại đó do  ,
,  gây ra bằng không luôn nằm gần điện tích có độ lớn nhỏ hơn và nằm xa điện tích có độ lớn lớn hơn.
gây ra bằng không luôn nằm gần điện tích có độ lớn nhỏ hơn và nằm xa điện tích có độ lớn lớn hơn.
BÀI TẬP LUYỆN TẬP
1. Hai điện tích điểm q1 = 10-6C và q2 = 8.10-6C đặt tại hai điểm cố định A và B trong dầu (ε = 2). AB = 9cm. Xác định vị trí của điểm N mà tại đó điện trường triệt tiêu.
Đs: r1=3cm và r2=6cm
2. Hai điện tích điểm q1 = 4.10-6C và q2 = 36.10-6C đặt tại hai điểm cố định A và B trong dầu (ε = 2). AB = 16cm. Xác định vị trí của điểm M mà tại đó điện trường tổng hợp bằng không.
Đs: r1=4cm và r2=12cm
3. Hai điện tích điểm q1 = 9.10-7C và q2 = -10-7C đặt tại hai điểm cố định A và B trong không khí. AB = 20cm. Xác định vị trí của điểm M mà tại đó điện trường tổng hợp bằng không.
Đs: r2 = 10cm r1=30cm
4. Cho hai điện tích q1, q2 đặt tại A và B , AB = 2cm. Biết 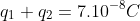 và điểm C cách q1 6cm, cách q2 8cm sao cho cường độ điện trường E = 0. Tìm q1 và q2 ?
và điểm C cách q1 6cm, cách q2 8cm sao cho cường độ điện trường E = 0. Tìm q1 và q2 ?
Đs: 
5. Tại hai điểm cố định A và B trong chân không cách nhau 60cm có đặt hai điện tích điểm q1 = 10-7C và q2 = -2,5. 10-8C.
a) Xác định vị trí của điểm M mà tại đó điện trường tổng hợp bằng không.
b) Xác định vị trí tại điểm N mà tại đó vecto cường độ điện trường do q1 gây ra có độ lớn bằng vecto cường độ điện trường do q1 gây ra. (chỉ xét trường hợp A,B,N thẳng hàng)
c) Xác định điểm P nằm trên đường thẳng AB mà tại đó 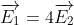 .
.
Đs:
a) r1=120cm và r2=60cm
b) Có hai vị trí : r1=120cm và r2=60cm và r1=40cm và r2=20cm
c) P nằm trên đường trung trực của AB

cùng phương, cùng chiều với
.
cùng phương, ngược chiều với
.
với k = 9.109
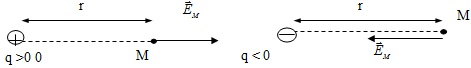
thì vector cường độ điện trường tổng hợp do các điện tích trên gây ra tuân theo nguyên lý chồng chất điện trường
.
, trong đó k = 9.109Nm2C-2.
.
bằng các vecto.
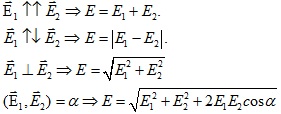
= 16. Điểm có cường độ điện trường như câu a cách điện tích bao nhiêu?.
cm

do điện tích q; q2 gây ra tại M có:
cùng phương, cùng chiều với
nên ta có E = E1M + E2M =
cùng phương, ngược chiều với
nên ta có
Cvà q2 = -10
C cách nhau 40 cm trong chân không.

là vecto cường độ điện trường do q1 và q2 gây ra tại C.
AC = 40 + x, có :
C đặt tại điểm đó ?
, độ lớn
cùng hướng với
; Nếu q < 0 thì
ngược hướng với
![]()
(1)
(2)
(3)
ngược hướng với
và có độ lớn:
... của mỗi điện tích điểm gây ra tại điểm mà bài toán yêu cầu. (Đặc biệt chú ý tới phương, chiều)
cùng hướng với
:
cùng hướng với
:
ngược hướng với
:
cùng hướng với
:
hợp với
một góc
xác định bởi:
:
hợp với
một góc


)
đặt ở A, C, hai điện tích
đặt ở B’ và D’. Tính độ lớn cường độ điện trường tại tâm O của hình lập phương. (ĐS:
)